Análisis comparativo del comportamiento estructural de una edificación de cuatro niveles con base fija y base aislada

Comparative analysis of the structural behavior of a four-story building with a fixed base and an isolated base

Análise comparativa do comportamento estrutural de um edifício de quatro pavimentos com base fixa e base isolada

Katherine Niquen [1], Genner Villarreal[2], Vicente Niquen[3]

Recibido: 17/05/2023 Aceptado: 15/09/2023

Resumen. - El aislamiento sísmico en edificaciones esenciales es una tecnología innovadora que modifica la respuesta estructural mediante el incremento de amortiguamiento y disminución de la rigidez en la interfaz de aislamiento de una estructura. En el artículo se compararon los resultados de una estructura convencional con cimentación fija y una estructura desacoplada en dos partes: cimentación y superestructura mediante una interfaz de aislamiento, ambas sometidos a una seudoaceleración equivalente a sismos raros. La determinación de las propiedades mecánicas de los dispositivos se desarrolló en base a los fundamentos matemáticos que relacionan masa, periodo y rigidez establecidos por Skinner, Robinson y McVerry (1993), Naeim & Kelly (1999), Kelly & Konstantinidis (2011) y Constantinou et. al, (2007). Se consideró una estructura convencional inicialmente diseñada con un sistema sismorresistente en pórticos de concreto y albañilería confinada, perteneciente al Centro de Salud I-3 Andrés Araujo Morán en la Región Tumbes, Perú. En la interfaz se propuso dispositivos de alto amortiguamiento con núcleo de plomo LRB (Lead Rubber Bearing) con un amortiguamiento crítico de 15% y un factor de amortiguamiento equivalente de 〖β〗_M=1.35. En los resultados obtenidos se aprecia que el periodo de la estructura se incrementó de T=0.47s a T=2.462s en comparación a la estructura convencional. Mientras que en el drift se redujo en un 57.45% de δ=0.0047 a δ=0.0020 con lo cual se concluye que la estructura se encuentra dentro de la funcionalidad continua de acuerdo a HAZUS (FEMA,2020).

Palabras clave: Aislamiento sísmico, rigidez, amortiguamiento, deriva, funcionalidad continua.

Summary. - Seismic isolation in essential buildings is an innovative technology that modifies the structural response by increasing damping and decreasing stiffness at the isolation interface of a structure. The article compared the results of a conventional structure with a fixed foundation and a decoupled structure in two parts: foundation and superstructure through an isolation interface, both subjected to a pseudo-acceleration equivalent to rare earthquakes. The determination of the mechanical properties of the devices was developed based on the mathematical foundations that relate mass, period and rigidity established by Skinner, Robinson and McVerry (1993), Naeim & Kelly (1999), Kelly & Konstantinidis (2011) and Constantinou. et. al, (2007). A conventional structure initially designed with an earthquake-resistant system in concrete frames and confined masonry, belonging to the I-3 Andrés Araujo Moran Health Center in the Tumbes Region, Peru, was considered. At the interface, high damping devices with lead core LRB (Lead Rubber Bearing) were proposed with a critical damping of 15% and an equivalent damping factor of β_M=1.35. In the results obtained, it can be seen that the period of the structure increased from T=0.47s to T=2.462s compared to the conventional structure. While in the drift it was reduced by 57.45% from δ=0.0047 to δ=0.0020, with which it is concluded that the structure is within the continuous functionality according to HAZUS (FEMA, 2020).

Keywords: Seismic isolation, stiffness, damping, drift, continuous functionality.

Resumo. - O isolamento sísmico em edifícios essenciais é uma tecnologia inovadora que modifica a resposta estrutural aumentando o amortecimento e diminuindo a rigidez na interface de isolamento de uma estrutura. No artigo foram comparados os resultados de uma estrutura convencional com fundação fixa e uma estrutura desacoplada em duas partes: fundação e superestrutura através de uma interface de isolamento, ambas submetidas a uma pseudo-aceleração equivalente a raros terremotos. A determinação das propriedades mecânicas dos dispositivos foi desenvolvida com base nos fundamentos matemáticos que relacionam massa, período e rigidez estabelecidos por Skinner, Robinson e McVerry (1993), Naeim & Kelly (1999), Kelly & Konstantinidis (2011) e Constantinou et. . al, (2007). Foi considerada uma estrutura convencional, inicialmente projetada com sistema antissísmico em pórticos de concreto e alvenaria confinada, pertencente ao Centro de Saúde I-3 Andrés Araujo Morán na Região de Tumbes, Peru. Na interface foram propostos dispositivos de alto amortecimento com núcleo de chumbo LRB (Lead Rubber Bearing) com amortecimento crítico de 15% e fator de amortecimento equivalente de β_M=1,35. Nos resultados obtidos pode-se observar que o período da estrutura aumentou de T=0,47s para T=2,462s em relação à estrutura convencional. Já na deriva foi reduzido em 57,45% de δ=0,0047 para δ=0,0020, o que conclui que a estrutura está dentro da funcionalidade contínua segundo HAZUS (FEMA,2020).

Palavras-chave: Isolamento sísmico, rigidez, amortecimento, deriva, funcionalidade contínua.

1. Introducción. – Una de las zonas con mayor actividad sísmica del planeta, es el borde occidental de América del Sur (Tavera et al., 2014), por la presencia de la Placa de Nazca y la Placa Sudamericana que generan un proceso geotécnico de convergencia y subducción, dando como resultado un alto índice de sismicidad. Esta naturaleza sísmica exige estructuras con un nivel mayor de seguridad con la finalidad de resistir eventos sísmicos severos (sismos de diseño) y eventos sísmicos raros (sismo máximo considerado). Según la norma E.030, mediante el diseño sismorresistente se tiene como principal objetivo proteger la vida, sin embargo, se reconoce que no es factible proteger a la estructura frente a los diversos tipos de embates sísmicos, por tanto, no exime del colapso de la estructura. Por otra parte, los criterios de funcionalidad continua sugerido por el Ph.D. Zayas (2017) para estructuras esenciales parten desde otro enfoque buscando la protección completa de la estructura y por tanto la vida de los ocupantes, promoviendo un estándar de continuidad de las estructuras después de eventos sísmicos severos y raros, esto lleva a cambiar la finalidad del diseño para conservar la operatividad de las edificaciones que sean categorizados como esenciales, asegurando su funcionamiento después de cualquier tipo de sismo.

En este contexto, la utilización del aislamiento sísmico para las estructuras en zonas de peligro sísmico Z_4 y Z_3 de Perú se han reglamentado como obligatorios para edificaciones con Categoría A1, los mismos que se clasifican como establecimientos del sector salud del segundo y tercer nivel, es decir su uso es obligatorio en hospitales tipo I y tipo II en las categorías establecidas por el Ministerio de Salud Peruano (MINSA), sin embargo, no están reglamentadas para estructuras de menor categoría y dimensión como los centros de salud, puestos de salud, institutos de salud, clínicas y otros, siendo estas edificaciones las que más se construyen en el país. Se considera que esta limitación del uso de los sistemas de aislamiento sísmico se debe a diversos factores, como el desconocimiento de los beneficios frente a una estructura convencional, la posibilidad del alto costo del sistema de aislamiento en proyectos de menor inversión a los hospitales de Categoría I, en este contexto la unidad formuladora de proyectos del Gobierno Regional de Tumbes, presentó la oportunidad de mejorar y ampliar los servicios prestados por el Centro de Salud I-3 Andrés Araujo Morán en la Región de Tumbes, mediante un Proyecto de Inversión pública, donde se plantea que, la estructura de la edificación puede ser propuesta con un sistema convencional sismorresistente de albañilería confinada y pórticos de concreto, que pueda cumplir con un criterio sismorresistente en el análisis estructural bajo la norma E.030.

En este aspecto, se procedió a demostrar que la utilización de una interfaz de aislamiento sísmico con dispositivos LRB, dado que se caracterizan por su flexibilidad y capacidad de absorción de energía (Wamanrao & Narayan, 2015) pueden reducir significativamente en términos porcentuales y comparativos parte de las fuerzas sísmicas, la deriva (drift) y deformaciones de entrepiso que se presentan en la estructura en un evento sísmico raro, incluso logrando un comportamiento dentro de los criterios para la funcionalidad continua por HAZUS (FEMA, 2020). Mediante un análisis comparativo se determinó el comportamiento estructural de la edificación, analizando la variación en el periodo de vibración de la estructura y principalmente el drift que es el criterio usado por las diversas normas para evaluar el comportamiento estructural.

Se debe indicar que la propuesta inicial para el Centro de Salud desarrollado por la Unidad Formuladora, se realizó mediante tres edificios independientes o bloques regulares de cuatro niveles separados únicamente por una junta sísmica, estructurados con pórticos y muros de albañilería confinada, una estrategia de solución estructural frecuente en edificaciones de salud peruanas, por tanto, se obtuvieron tres estructuras con sus respectivos análisis. La propuesta realizada con aislamiento sísmico mediante dispositivos de alto amortiguamiento LRB, propone la unificación de estos tres edificios en un único bloque sobre el nivel de base que conecta con la interfaz de aislamiento. En la propuesta con aislamiento sísmico con dispositivos Lead Rubber Bearing (LRB), se incorporó un piso técnico según norma E.031, añadiendo el nivel de base a la estructura original, una interfaz de aislamiento con 63 dispositivos LRB y un sistema de dados de concreto para el empotramiento de los dispositivos. Mediante el análisis estático se determinó que el desplazamiento máximo para la estructura es D_M=0.3134 m y el desplazamiento total máximo es D_TM=0.3658 m. Para el análisis dinámico modal espectral de la estructura con aislamiento sísmico se utilizó un espectro con seudoaceleración de S_aM=1.85g correspondiente a los factores establecidos en la norma E.030 y E.031 obteniendo un desplazamiento máximo en el centro de masa de D_TM=0.4125 m.

Para la verificación de resultados mediante análisis dinámicos no lineales de tiempo historia, se utilizaron cinco acelerogramas de eventos sísmicos representativos en Perú: Sismo de Lima de 1966, Sismo de Ancash de 1970, Sismo de Lima de 1974, Sismo de Arequipa de 2001 y Sismo de Ica de 2007, eventos sísmicos que representan el peligro sísmico actualmente especificado en la Norma Técnica E.030 para zonas Z_4 con aceleración de 0.45g. El procedimiento y metodología de escalamiento sísmico se realizó considerando los criterios de la norma E.031 que sugiere que se realice un procedimiento de escalamiento del sismo a un espectro para un sismo máximo considerado SMC considerando un factor de reducción R=1 para la estructura y teniendo en cuenta las propiedades modificatorias mínimas y máximas de los dispositivos establecidas en la norma americana ASCE SEI 7/16 y norma peruana E.031.

2. Fuerzas sísmicas para el análisis sísmico. – Las fuerzas sísmicas representadas por la seudoaceleración utilizadas en el análisis sísmico de las estructuras se definió mediante lo especificado en las Normas Técnicas peruanas para Diseño Sismorresistente E.030, y la Norma Técnica E.031. La ubicación física de la estructura es en la costa peruana, región de Tumbes categorizada como zona de alto peligro sísmico Z_4 con una aceleración sísmica de 0.45g.

Los parámetros del espectro de diseño se obtuvieron mediante la prueba de penetración estándar SPT del estrato del suelo, que definieron un suelo flexible y que cotejando en la norma de diseño sismorresistente peruana E.030 (Tabla 3 y 4), establece los siguientes parámetros de sitio (S,TP,TL): S=1.10 , T_P=1.0 y T_L=1.6.

Respecto al sistema estructural, la norma E.030 establece los coeficientes básicos de reducción para el sistema estructural por albañilería confinada como R_o=3 y aporticado como R_o=8.

Respecto al coeficiente sísmico C, se determinó mediante las ecuaciones de la norma E.031, Articulo 14.4.

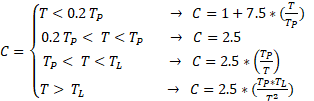(1)

En la ec.1, se determinó que el coeficiente sísmico para la estructura con base fija es C=2.5 al verificar que el periodo obtenido T=0.47s se encuentra dentro del intervalo 0.2 T_p<T〖<T〗_L. El factor de uso por la categoría de la edificación se consideró como U=1 (Tabla 5 de la Norma E.030) teniendo en cuenta que la estructura será modelada con aislamiento sísmico. Con estos datos se determinó la seudoaceleración elástica (S_ae) mediante ec.2:

(2)

Reemplazando los valores de los parámetros de zona sísmica, coeficiente sísmico, suelo y factor de reducción se determinó que la seudoaceleración elástica es:

Para verificar las derivas de entrepiso (drift) en la norma E.030 se menciona para la estructura con base fija que, estos deben determinarse en el rango inelástico, por lo cual se utilizó la seudoaceleración inelástica () determinada mediante:

(3)

En la ecuación 3 se tiene establecido que se aplica a estructuras regulares y a estructuras irregulares. Cabe señalar que se determinó que la estructura es regular, mediante el análisis de los periodos en las direcciones traslacionales y rotacionales y diferencias de rigidez de entrepiso. Se obtuvo:

Se utilizó la seudoaceleración para determinar la deformación lateral inelástica en la estructura con el sistema convencional con los criterios normativos de la norma peruana. Además, en la ecuación 2 se debe señalar que al considerar el factor de reducción básico como , se obtiene la seudoaceleración para un sismo de diseño ().

Para el caso del análisis de la estructura con el sistema de aislamiento se utilizó un espectro inelástico establecida mediante la ecuación de la norma técnica E.031, en su item 14.4.

(4)

Remplazando los valores en la ec.4 se obtuvo:

En la Figura I se aprecia los cuatro espectros de seudoaceleración relacionados a la estructura. El sismo máximo considerado se utilizó para el análisis de las derivas de entrepiso (drift) de la estructura aislada.

Figura I.- Espectros de seudoaceleración para el análisis sísmico.

3. Modelamiento y análisis de la estructura convencional. –

3.1. Niveles de la estructura. – La edificación tomada para la investigación es un centro de salud, categorizado como estructura esencial. La estructura original se encuentra constituida por tres bloques estructurales, con un sistema de pórticos y muros de albañilería que contribuyen a la rigidez en las direcciones con mayor desventaja, con un sistema modelado con distancias exactas entre los ejes de 6.0 m en la dirección XX y dirección YY. Se propusieron de acuerdo a los criterios de la norma E.030 considerando que la estructura cuenta con cuatro niveles con altura de entrepiso de 4.2 m con una altura acumulada de 16.8 m.

En la Figura II se puede apreciar el detalle arquitectónico de la primera planta en el cual se aprecian los tres bloques estructurales principales del proyecto, el bloque achurado en color plomo es para servicios complementarios con un solo nivel, por tanto, no se consideró como parte integrante de la estructura con aislamiento sísmico.

Figura II.- Distribución en plantas del centro de salud.

En la Figura III se puede apreciar el diseño estructural original con los respectivos ejes estructurales y los pórticos de concreto para los tres bloques, la propuesta original elaborada por los proyectistas considera que entre bloques existe una junta sísmica.

Figura III.- Sistema estructural en Pórticos.

En la Tabla I se aprecian las alturas de los tres bloques de la estructura inicial, con una altura de 16.8 m con cuatro niveles y azotea. El nivel de azotea cuenta con una altura de 3.00 m. sin embargo, carece de diafragma rígido (losa) por lo cual no se consideró para analizar las derivas.

Niveles	Altura (metros)	Acumulado (metros)
Azotea	3.0	19.8
Story4	4.2	16.8
Story3	4.2	12.6
Story2	4.2	8.4
Story1	4.2	4.2

Tabla I. Altura de entrepiso de los bloques

3.2. Modelamiento de la estructura con base fija. – Por aspectos comparativos, inicialmente se procedió a modelar los tres bloques independientes para verificar la respuesta estructural de cada bloque con un análisis modal espectral. Los bloques de la estructura fueron modelados independientemente como se propuso en la propuesta estructural original con base fija, los bloques se modelaron con las siguientes propiedades de los materiales:

· Resistencia a la compresión del concreto : f’c=210 kgf/cm2

· Resistencia a la compresión de la albañilería : f’m=140 kgf/cm2

· Resistencia del acero : f’y=4200 kgf/cm2

· Módulo de elasticidad del concreto : Ec= 2188.2 kgf/mm2

· Coeficiente de Poisson : µ= 0.20

· Peso específico del Concreto Armado : γ_CA=2400 kgf/cm3

En la Figura IV se aprecian los tres bloques estructurales originales modelados en el software de análisis y se aprecian los pórticos y los muros de albañilería que añaden rigidez a la estructura:

Figura IV.- Modelos estructurales de los bloques 01,02 y 03.

En la Figura V se aprecia el modelo con los tres bloques estructurales integrados en una sola propuesta estructural, en el modelo se eliminó la junta sísmica que caracterizaba a la propuesta inicial y los pórticos que se duplicaban. En el modelo se procedió a incorporar las cargas establecidas en la norma E.020 para edificaciones de salud. Dentro de los criterios estructurales se asignó al modelo los correspondientes diafragmas rígidos, el empotramiento en la base, la incorporación del brazo rígido para uniones columna-viga.

Figura V.- Modelo estructural integrado con base fija..

3.3. Resultados del análisis dinámico.

Periodo de las estructuras con la base fija

Para el análisis modal espectral, se consideraron 12 casos modales, tres por nivel. Se verificó además que la participación modal de la masa en los doce casos modales supere el 90% tal como lo señala y lo requiere la norma E.030. En la Tabla II se aprecian los periodos de los tres bloques y del modelo integrado. Se pudo verificar que los tres bloques de la propuesta inicial tienen periodos muy similares (, mientras que en el modelo integrado el periodo disminuye (. En el caso del modelo integrado, modeladas con las mismas secciones estructurales de los tres bloques, la rigidez se incrementó disminuyendo el periodo de vibración. El periodo del modelo integrado se consideró como parámetro comparativo para la estructura con aislamiento sísmico.

		Bloque 01	Bloque 02	Bloque 03	Estructura única
Caso	Modo	T(s)	T(s)	T(s)	T(s)
Modal	1	0.597	0.590	0.553	0.470
Modal	2	0.437	0.441	0.443	0.373
Modal	3	0.220	0.394	0.364	0.292

Tabla II. Periodo de las estructuras

Deriva de entrepiso en la estructura convencional

Después del modelamiento con todos los criterios hipotéticos requeridos, se procedió al análisis modal espectral, con una seudoaceleración en el rango elástico de 0.1547g. Esta seudoaceleración proporcionó los resultados de deformación lateral en el rango elástico, sin embargo, en la norma E.030 se señala que estos resultados deben ser amplificados por 0.75R para obtener las deformaciones en el rango inelástico, por lo cual los resultados de deformación lateral o deriva son similares a los obtenidos en un análisis con una seudoaceleración de . Las derivas obtenidas para los tres bloques y la estructura integrada se aprecian en la Tabla III. Los resultados demuestran que el drift no supera la máxima deformación permisible de establecida en la norma E030 para estructuras convencionales. La máxima deriva obtenida en la estructura integrada es en la dirección XX del modelo. En ninguno de los casos se obtuvo un drift por debajo del para categorizar a la estructura dentro de la funcionalidad continua según lo señalado en HAZUS (FEMA, 2020).

Story	Bloque 01		Bloque 02		Bloque 03		Estructura única
	XX	YY	XX	YY	XX	YY	XX	YY
Story4	0.0049	0.0033	0.0052	0.0045	0.0044	0.0035	0.0044	0.0035
Story3	0.0050	0.0036	0.0061	0.0045	0.0047	0.0037	0.0047	0.0037
Story2	0.0040	0.0033	0.0046	0.0014	0.0042	0.0033	0.0042	0.0033
Story1	0.0010	0.0020	0.0031	0.0008	0.0024	0.0018	0.0024	0.0018

Tabla III. Deriva de entrepiso en el modelo convencional

4. Estructura propuesta con sistema de aislamiento y propiedades de los dispositivos. - Los bloques de la estructura con aislamiento cuentan con las mismas propiedades de materiales, como resistencia a la compresión, módulo de elasticidad, peso específico, utilizados en el modelo con base fija. En la Figura VI se aprecia el modelo matemático con la interfaz de aislamiento incorporado y los 63 dispositivos de aislamiento que en el modelo matemático se modelan como Links con propiedades de rigidez y amortiguamiento.

Figura VI.- Modelo estructural con interfaz de aislamiento..

En la Tabla IV se aprecia la altura de los entrepisos, la azotea, el nivel de base y capiteles, la interfaz de aislamiento y altura de los pedestales de concreto. Además, se aprecia el peso sísmico que se determinó mediante la combinación establecida en la norma E.031 definida como “Carga promedio” igual a:

(5)

La carga promedio o peso sísmico se determinó mediante el modelamiento de la estructura, mediante el peso sísmico estimado se determinaron las propiedades de rigidez y amortiguamiento requeridos por la estructura, se estableció que la estructura tiene un peso sísmico obtenido con una combinación de carga en el software mediante la ec.5. Al dividir el peso sísmico de la estructura entre los 63 dispositivos se obtuvo una carga por dispositivo equivalente a .

Story	Altura	(Ux -Uy)
	m	Kgf	Tonf
Azotea	3.00	537101.21	537.101
Story4	4.2	1419940.54	1419.941
Story3	4.2	1444331.36	1444.331
Story2	4.2	1467283.58	1467.284
Story1	4.2	1508479.18	1508.479
Nivel de Base y capitel	1.2	2602052.12	2602.052
Interfaz de aislamiento	0.35	146386.8
Pedestales de concreto	1.2	146386.8
Base	0	130636.8
Peso total sobre la interfaz de aislamiento			8979.19

Tabla IV Niveles y peso sísmico de la estructura sobre la interfaz

4.1. Diámetro y altura del caucho del dispositivo. - Para estimar estas dimensiones del dispositivo, se procedió a determinar los desplazamientos máximos y máximo total en el nivel de aislamiento.

Desplazamiento para un sismo máximo considerado

El predimensionamiento de los dispositivos a utilizar, se realizó considerando un desplazamiento de tipo hipotético, calculado con la ecuación del Art. 20 “Desplazamientos laterales considerados para el diseño” de la norma E.031, que proporciona el desplazamiento traslacional máximo para un sismo máximo.

(6)

Dónde:

Seudoaceleración para un SMC (en unidades de “g”)

: 3s Periodo efectivo de la estructura con aislamiento sísmico

Factor de amortiguamiento (15% de amortiguamiento crítico del dispositivo)

Considerando la seudoaceleración, el periodo objetivo y el factor de amortiguamiento en la ec.6, se obtuvo un desplazamiento máximo :

Desplazamiento total para un sismo máximo considerado

Mediante el desplazamiento máximo considerado, se determinó el desplazamiento total máximo , que incorpora los desplazamientos torsionales al desplazamiento máximo mediante la ecuación del Artículo 20, Item 20.3 de la norma E031:

(7)

En la ecuación 7 se consideran las dimensiones de la estructura:

:

: (Distancia del centro de rigidez al punto más alejado de la estructura)

: (Excentricidad, 5% del lado mayor de la edificación).

: Lado menor de la edificación

: Lado mayor de la edificación

: Razón entre el periodo traslacional efectivo de la estructura y el periodo rotacional de la edificación. La norma E031 menciona que no requiere ser menor que la unidad, se consideró 1.15.

Reemplazando valores en la ec.7 de desplazamiento total se obtuvo:

Rigidez horizontal del dispositivo

La rigidez del caucho del dispositivo se determinó mediante la ecuación de rigidez que relaciona la masa, el periodo de la estructura y su rigidez que se deriva de la Ley de Hooke.

(8)

Donde:

: Rigidez del dispositivo en la dirección horizontal

: 142.53 ton (carga promedio sobre el dispositivo)

: 3.0 s. (Periodo de la estructura aislada)

Mediante los valores reemplazados en ec.8 se obtuvo la rigidez en como se aprecia a continuación:

Se debe mencionar que la rigidez calculada es referencial únicamente para el caucho, y se utilizó para determinar un diámetro aproximado de caucho. La rigidez efectiva final se determinó con la incorporación del núcleo de plomo.

Determinación de la altura del caucho del dispositivo

La altura del caucho del dispositivo se determinó mediante el desplazamiento total máximo que se calculó para la estructura, como se solicita en la norma E.031 en el Anexo II, con la ecuación de “deformación por corte” que se aprecia a continuación:

(9)

Donde:

: 2 (Deformación de corte directa que oscila entre )

: Altura del caucho

: 0.366 m (Desplazamiento total máximo)

En la ec. 9 se consideró que la deformación de corte directa es igual . Despejando la altura de caucho de la ecuación se obtuvo:

Diámetro del dispositivo

La rigidez de un dispositivo de aislamiento, se encuentra relacionado al área del caucho, la capacidad elástica del material definida como módulo de corte (macropropiedad del elastómero determinado de manera experimental) y la altura del caucho. Estas relaciones definidas por autores como Kelly (1993, p.108) y Kammerer et al. (2019, p. 4-1) se verifican en la siguiente ecuación:

(10)

Donde:

: 0.625 kN/mm

: 0.4 N/mm2 (Caucho blando, proveedores tensa y FIP)

: Área del dispositivo sometida a compresión axial

: 0.183 m

El módulo de corte para dispositivos estándar con un caucho blando equivale a . Por tanto, reemplazando y despejando el área “A” en la ec.10 se obtuvo:

Determinando el diámetro del dispositivo se obtuvo:

, donde

Reemplazando:

=

El diámetro inicial del caucho requerido se consideró en , que después debe verificarse experimentalmente para determinar la estabilidad del dispositivo (Kelly & Marsico,2010).

4.2. Propiedades mecánicas del dispositivo de aislamiento

Fuerza característica Q del dispositivo

En un dispositivo LRB (Lead Rubber Bearing), la fuerza característica Q está en función al área de la sección transversal del núcleo de plomo a utilizar, en vista que el esfuerzo de fluencia del plomo (tensión de fluencia) oscila entre 85 kg/cm2 – 115 kg/cm2 o su equivalente en MPa aproximadamente de 8 a 10 MPa (Lancu, Gillich & Vasile, 2012, p. 238). Las láminas metálicas del dispositivo confinan el núcleo de plomo y obligan al plomo a deformarse en corte (Kamrava, 2015). El plomo inicialmente presenta un nivel alto de rigidez, sin embargo, cuando la deformación lateral supera el 6.7% de la deformación angular, la rigidez del dispositivo dependerá de las propiedades del caucho, esto implica que se tenga una diferencia alta entre rigidez efectiva y rigidez post fluencia. Oikonomou et al. (2016) señalan que la fuerza característica del dispositivo con núcleo de plomo es equivalente a:

(11)

Dónde:

: Fuerza característica

: (Área transversal del núcleo de plomo)

: (Tensión de fluencia del plomo)

Después de seguir un procedimiento iterativo por aproximación para obtener el diámetro del núcleo de plomo, se determinó que un diámetro de mejora la rigidez del dispositivo considerablemente. Por tanto, el área de la sección transversal del núcleo de plomo se obtuvo con la ec.12:

: (12)

:

La tensión de fluencia del plomo considerado es equivalente a para dispositivos LRB, lo cual permitirá lograr el periodo efectivo deseado de la estructura con aislamiento. Hallando con esto datos la fuerza característica con la ec.11, se tiene:

Rigidez post fluencia

Después de entrar en desplazamiento, el dispositivo pierde la rigidez inicial aportada por el núcleo de plomo, y se genera una rigidez post fluencia, que se determinó únicamente en función a las características y área transversal del caucho mediante la ecuación 13.

(13)

Donde:

: Rigidez post fluencia en kN/mm

: 0.4 N/mm2 (Módulo de corte para caucho blando)

: Área del caucho menos el área del plomo

: 0.183 m

Hallando el área “A” mediante la diferencia de área entre el caucho y plomo se tiene:

(14)

Donde:

: 0.60 m Diámetro externo (caucho)

: 0.15 m Diámetro interno (núcleo de plomo)

Se obtuvo un área “A” mediante la ec. 14 como se aprecia a continuación:

Con el módulo de corte del caucho y el área estimada, se determinó la rigidez post fluencia:

Cálculo de la rigidez efectiva

La rigidez efectiva , conocida como la rigidez efectiva del dispositivo Se calcula mediante la siguiente ecuación establecida en Naeim y Kelly (1999), Constantinou, Whittaker, Kalpakidis, Fenz y Warn (2007, p. 22), en la cual se considera la rigidez postfluencia, la fuerza característica y el desplazamiento total máximo, como se aprecia en la siguiente ecuación:

(15)

Dónde:

: Rigidez post fluencia

: (Fuerza característica Q)

: (Desplazamiento máximo total del dispositivo)

Calculando mediante la ec.15:

Cálculo del desplazamiento de fluencia

es el yield displacement (Usta, 2021) o desplazamiento de fluencia y se define mediante la fuerza característica Q dividida por la diferencia de la rigidez inicial y rigidez post fluencia como se observa en la ecuación 15. La rigidez inicial o elástica se asume que es equivalente a 10 veces la rigidez post fluencia, en vista que no se puede calcular experimentalmente ni matemáticamente, dado que a un desplazamiento de fluencia = 0 la rigidez no es calculable.

(16)

Dónde:

(Fuerza característica)

m

Reemplazando en la ec.16 se obtuvo:

Energía disipada en cada ciclo por el dispositivo

Uno de los medios más eficaces de proporcionar un nivel sustancial de amortiguación a una estructura, es a través de la disipación de energía histerética. El término "histérico" se refiere al desfase en las curvas de carga y descarga bajo una carga cíclica (Mayes & Naeim, 2003). El gráfico histerético que se aprecia es una idealización bilineal y simplificada de la deformación que sufre un dispositivo de aislamiento frente a las fuerzas sísmicas. Teóricamente la energía disipada por ciclo es equivalente al área que genera bajo la curva histerética en cada ciclo de disipación de energía, en un modelo de aproximación bilineal del comportamiento de la ley histerética (Zellat & Kadri, 2015).

En la Figura VII el área generada por los desplazamientos es la energía disipada por ciclo histerético de carga (Stojadinovic, s/f, p. 47). Se puede apreciar que en el modelo el desplazamiento de fluencia da lugar a la rigidez de fluencia y el desplazamiento máximo da lugar a la rigidez efectiva del dispositivo.

Figura VII.- Gráfico de histéresis. Adaptado de Constantinou (2007, p.21).

Mediante la ec.17 de Constantinou et al. (2007, p. 22) que relaciona la fuerza característica Q, con los desplazamientos máximos y desplazamiento de fluencia se puede determinar la energía disipada por ciclo histerético, como se aprecia a continuación:

(17)

Dónde:

: Energía disipada en kN.m

: (Fuerza característica Q)

: (Desplazamiento máximo total estático en m)

: (Desplazamiento de fluencia en mm)

Con los datos, se obtuvo la energía disipada con la ec.17:

Amortiguamiento crítico del dispositivo

Constantinou et al. (2007, p. 22) menciona que el porcentaje de amortiguamiento critico que un dispositivo aporta en una estructura se puede determinar mediante la siguiente ecuación:

(18)

Dónde:

: Amortiguamiento crítico del dispositivo en %

: 198.87 kN.m (Energía disipada por ciclo histerético)

: 0.981 kN/mm (Rigidez efectiva del dispositivo)

: 0.366 (Desplazamiento máximo total estático en m)

Remplazando valores en ec.18 se obtiene:

El dispositivo propuesto con el diámetro de caucho y núcleo de plomo estimado, que determinan la rigidez efectiva del dispositivo, pueden proporcionar un amortiguamiento efectivo de 24.07% del amortiguamiento crítico.

Rigidez elástica

La rigidez inicial o elástica es equivalente a la fuerza característica requerida para lograr un desplazamiento de fluencia inicial, más la rigidez post fluencia del dispositivo, como se aprecia en la ecuación. La rigidez inicial elástica es equivalente a:

(19)

Por tanto, se obtuvo mediante la ec.19:

Fuerza de fluencia

La fuerza de fluencia es igual a la fuerza característica Q más el producto de la rigidez post fluencia que multiplica al desplazamiento de fluencia . Por tanto, se calcula con la siguiente ecuación:

(20)

Remplazando los valores en ec.20 para obtener la fuerza de fluencia se obtuvo:

El ratio de rigidez, se determinó mediante la relación de rigidez post fluencia y rigidez inicial o elástica, se obtuvo un ratio de:

Periodo y frecuencia angular de la estructura aislada

La norma E.031 en el Artículo 20, item 20.2 señala que el periodo efectivo de la estructura con aislamiento sísmico es igual a y se determina con la siguiente ecuación:

(21)

Dónde:

: Periodo del edificio con aislamiento

: 8979(Peso o Carga promedio según la E.030 en kN)

: 6.31(Rigidez efectiva del sistema)

: 9800 (Aceleración de la gravedad)

Remplazando valores en la ec.21 se obtuvo:

Con el periodo real se determinó la frecuencia angular del sistema, que permitió determinar el amortiguamiento efectivo. La frecuencia angular está dada por la siguiente ecuación:

(22)

Remplazando valores en la ec.22 se obtuvo:

Amortiguamiento efectivo del aislador

El amortiguamiento efectivo del sistema se calcula teniendo en cuenta la frecuencia angular de la estructura mediante la siguiente ecuación:

(23)

Dónde:

: Amortiguamiento efectivo del aislador

: 198.87 kN.m (Energía disipada por ciclo histerético)

: (Desplazamiento máximo del sistema)

: (frecuencia angular)

Remplazando valores en la ec.23 se obtuvo:

Cuadro resumen de las propiedades mecánicas del dispositivo

Los dispositivos se modelaron en el software de análisis como elementos de tipo Link, en los que se ingresaron las propiedades mecánicas de los dispositivos con núcleo de plomo calculados mediante las ecuaciones, cuyos resultados ya resumidos se aprecian en la Tabla V.

Propiedades mecánicas	Unidades	Lead Rubber Bearing LRB
Rigidez efectiva Keff	kN/mm	0.9814
Rigidez inicial Ke	kN/mm	5.7932
Rigidez post fluencia kd	kN/mm	0.5793
Relación r. inic. / r. post	ratio	0.097
Fuerza Característica Q	kN	147.19
Fuerza de fluencia	kN	163.54
Energía disipada	kN.m	198.87
Amortiguamiento efectivo C	kN.seg/mm	0.18021

Tabla V Propiedades mecánicas de los dispositivos

Incorporación de las propiedades mecánicas en los dispositivos

Los dispositivos se generaron como elementos link de tipo Rubber Isolator, a los cuales se incorporaron las propiedades no lineales calculadas como las propiedades mecánicas del dispositivo. En la Figura VIII se observa el cuadro de ingreso de las propiedades para los elementos link, y el modelo con la interfaz de aislamiento en la cual se procedió a incorporar los dispositivos, adicionando previamente el nivel de base con los dados de concreto.

Figura VIII.- Incorporación de las propiedades mecánicas y modelo final

5. Resultados del análisis de la estructura con aislamiento. – Para obtener las deformaciones en el rango inelástico, se utilizó el espectro elaborado para el sismo raro o sismo máximo considerado con un valor de seudoaceleración equivalente a .

Periodo de la estructura con aislamiento

Madera, Marulanda & Thompson (2019) señalan que, mediante un sistema de aislamiento, el periodo fundamental de una estructura se incrementa y como consecuencia las seudo aceleraciones, la fuerza y energía sísmica disminuyen. En los resultados, en la Tabla VI se aprecia que el periodo de vibración de la estructura con aislamiento se incrementó hasta T(s)=2.462 s. Este resultado demuestra que la estructura tiene una menor frecuencia de vibración que la estructura con base fija.

Case	Mode	Period	Frequency	Circular Frequency	Eigenvalue
		sec	cyc/sec	rad/sec	rad²/sec²
Modal	1	2.462	0.406	2.5519	6.5124
Modal	2	2.456	0.407	2.5583	6.5448
Modal	3	2.301	0.435	2.7302	7.4541

Tabla VI. Periodos de la estructura con aislamiento

Desplazamiento relativo en el centro de masa con la base aislada

En la Tabla VII se aprecia que el desplazamiento relativo obtenido en la base de la estructura con aislamiento sísmico, en la dirección principal se obtuvo , en la dirección perpendicular se obtuvo .

Story	Load Case/Combo	Ux mm	Uy mm
Story4	Espectro_SMC_Max	438.37	435.71
Story3	Espectro_SMC_Max	432.47	430.36
Story2	Espectro_SMC_Max	425.59	425.41
Story1	Espectro_SMC_Max	417.96	420.96
Nivel de Aislamiento	Espectro_SMC_Max	411.46	412.60

Tabla VII. Desplazamiento en la base de la estructura con aislamiento

Deformación lateral permisible con aislamiento

En la Tabla VIII se verifica que las derivas con el sistema de aislamiento sísmico disminuyeron significativamente, logrando cumplir con la deriva máxima permitida en la norma E.031 definida como y con un desempeño en el rango de la funcionalidad continua según HAZUS (FEMA, 2020) por tener derivas menores a . En la dirección principal se obtuvo una deriva máxima de en el segundo nivel, mientras que en la dirección perpendicular se obtuvo , lo que significa una reducción del 57.45% del drift en comparación a la estructura convencional.

	Drift
Story	XX	YY	Norma E.031	HAZUS
Story4	0.0014	0.0013	0.0035	0.0025
Story3	0.0016	0.0012	0.0035	0.0025
Story2	0.0018	0.0011	0.0035	0.0025
Story1	0.0015	0.0020	0.0035	0.0025

Tabla VIII. Deriva de entrepiso de la estructura con aislamiento

6. Resultados de la estructura con aislamiento frente a un análisis time-history

Consideraciones previas para el análisis no lineal

Para realizar el análisis no lineal tiempo historia se consideraron registros sísmicos escalados con diversos periodos de retorno del evento sísmico, siendo el periodo de retorno de 2475 años el correspondiente al sismo máximo considerado (Lashgari, 2014). En el Item 15.6 de la norma E.031 se señala que el escalamiento de los sismos debe oscilar entre 0.75 y 1.25, donde es el periodo de la estructura aislada. Este rango debe ser calculado con el límite superior de las propiedades del dispositivo (0.75) y con el límite inferior de las propiedades del dispositivo (1.25).

Y cuando el registro sísmico es compatible con el espectro, se deberá escalar en el siguiente rango 0.2 y 1.25, donde el 0.2 se calcula con el límite superior de las propiedades de los dispositivos y el 1.25 se calcula con el límite inferior de las propiedades del dispositivo con núcleo de plomo.

Respecto a las propiedades inferiores y superiores, se calculan mediante los factores modificatorios de propiedades, que señalan que los dispositivos elastoméricos y con núcleo de plomo, pueden alterarse según las ecuaciones y .

En el artículo 13.3 de la norma E.031 se establece los factores modificatorios y ecuaciones de cálculo para las propiedades máximas y las propiedades mínimas:

Dónde:

: Factor modificatorio para determinar los valores máximos de las propiedades del aislador “considerando las condiciones ambientales y el envejecimiento” (Norma E.031)

: Factor modificatorio para determinar los valores mínimos de las propiedades del aislador “considerando las condiciones ambientales y el envejecimiento” (Norma E.031)

: Factor modificatorio para determinar los valores máximos de las propiedades del aislador “considerando las condiciones de temperatura, velocidad de carga, y scragging” (Norma E.031)

: Factor modificatorio para determinar los valores mínimos de las propiedades del aislador “considerando las condiciones de temperatura, velocidad de carga, y scragging” (Norma E.031)

Mediante estos factores modificatorios de las propiedades, se determinó un rango de emparejamiento para el espectro de escalamiento, al cual se sometieron los sismos seleccionados.

En la Tabla IX se puede observar los factores modificatorios (Fuente: Norma E.031 Art. 12.3.7) para dispositivos con núcleo de plomo, en este caso para fabricantes calificados de acuerdo a la normativa (proveedores que han estandarizado sus dispositivos mediante ensayos en laboratorios reconocidos):

Factor	Aislador de caucho con núcleo de Plomo
	K	Qd
Mínimo factor de modificación Max	1.3	1.5
Máximo factor de modificación Max	0.8	0.8

Tabla IX. Valores modificatorios para propiedades máximas y mínimas

Eventos sísmicos seleccionados para el análisis time-history

Para el análisis tiempo historia de la propuesta con aislamiento se consideraron cinco eventos sísmicos sucedidos en la costa peruana desde el año 1966 y que se mencionan cronológicamente: el sismo de Lima de 1966, el sismo de Ancash de 1970, el sismo de Lima de 1974, el sismo de Arequipa del 2001 y sismo de Ica del 2007.

En la Tabla X se muestra los datos técnicos de cada uno de los eventos considerados para el análisis tiempo historia, dentro de los que se observa la magnitud y la aceleración máxima de cada evento sísmico en ambas direcciones del sismo.

	Lima 1966	Ancash 1970	Lima 1974	Arequipa 2001	Ica 2007
Estación de registro	Parque de la Reserva	Parque de la Reserva	Parque de la Reserva	MOQ001	UNICA - ICA002
Latitud	-10.70	-9.36	-12.5	-16.08	-13.67
Longitud	-78.70	-78.87	-77.98	-73.77	-76.76
Frecuencia (Hz)	50	50	50	100	100
Fecha del sismo	17 de octubre de 1966	31 de mayo de 1970	03 de octubre de 1974	23 de junio de 2001	15 de agosto de 2007
Profundidad	25 km	64 km	13 km	33 km	40 km
Magnitud	8.1 Mw	6.6 Mw	6.6 Mb	6.9 Mb	7.0 ML
Número de registros	3283	2255	4899	19892	21807
Aceleración máxima EW en cm/s2	-180.56	-105.05	-194.21	-295.15	-272.82
Aceleración máxima NS cm/s2	-268.24	-97.81	180.09	219.99	333.66
Intervalo de tiempo (s)	0.02	0.02	0.02	0.01	0.01

Tabla X. Tabla descriptiva de los sismos seleccionados

En la Figura IX se aprecian los acelerogramas obtenidos del evento sísmico de Lima (1966) y Ancash (1970). En la Figura X se aprecian los acelerogramas obtenidos del evento sísmico de Lima (1974) y Arequipa (2001). En la Figura XI se observa el acelerograma obtenidos del evento sísmico de Ica (2007). Los eventos sísmicos seleccionados para el análisis correspondiente, cuentan con sus dos componentes Este-Oeste (EW) y Norte-Sur (NS).

Figura IX.- Eventos sísmicos ocurridos en Lima - 1966 y Ancash – 1970.

Figura X.- Eventos sísmicos ocurridos en Lima - 1974 y Arequipa – 2001.

Figura XI.- Evento sísmico ocurrido en Ica - 2007.

Escalamiento de los sismos a un sismo máximo considerado

El escalamiento de un evento símico empieza generando el espectro con un rango de periodos para su escalamiento, que permitirá emparejar las aceleraciones del evento sísmico con la ordenada espectral, dentro del rango para sismos compatibles.

Con los factores modificatorios, se determinaron los periodos fundamentales para la estructura con las propiedades modificatorias mínimas y las propiedades modificatorias máximas de los dispositivos, requeridos para determinar los rangos de escalamiento. Después del modelamiento se obtuvieron los siguientes periodos fundamentales que se aprecian en la Tabla XI.

Case	Modo	Máximo	Mínimo
		Periodo (s)	Periodo (s)
Modal	1	2.17	2.745
Modal	2	2.165	2.737
Modal	3	2.028	2.565

Tabla XI. Periodos fundamentales de la estructura con los factores modificatorios

Con los periodos fundamentales de la estructura, se determinó el periodo mínimo y máximo para el escalamiento de los eventos sísmicos, según lo mencionado en el Art. 15 de la Norma E.031.

(Periodo mínimo de escalamiento)

(Periodo máximo de escalamiento)

Por ende, los rangos son:

(Para el valor mínimo de escalamiento)

(Para el valor máximo de escalamiento)

En la Figura XII se observa la ordenada espectral de escalamiento y el intervalo generado por los periodos mínimo y máximo.

Figura XII.- Periodo mínimo y máximo para escalamiento.

El escalamiento de los sismos a la ordenada espectral, se realizó mediante el software SeismoMatch, logrando el emparejamiento de las aceleraciones sísmicas con la ordenada espectral. En la Figura XIII se aprecia los sismos escalados al espectro con los parámetros considerados.

Figura XIII.- Sismos emparejados al espectro de escalamiento.

Resultados del análisis no lineal tiempo historia

En la Tabla XII se aprecian los resultados del análisis time-history obtenidos con los cuatro casos de análisis sísmicos con el Sismo de Lima de 1966. Respecto a los desplazamientos en el centro de masa se obtuvo un desplazamiento máximo de para el componente EW y para el componente NS. Respecto al drift de entrepiso, se obtuvo una deriva máxima de para el componente EW y para el componente NS. En ninguno de los cuatro casos de análisis se llegó a superar el valor de , por lo cual se puede concluir que para este sismo la estructura se mantendría dentro de la funcionalidad continúa establecida en los criterios HAZUS (FEMA, 2020).

	Desplazamiento en el centro de masa (mm)				Drift
Story	Lima 1966 EW		Lima 1966 NS		Lima 1966 EW		Lima 1966 NS
	XX	YY	XX	YY	XX	YY	XX	YY
Story4	485.347	471.661	530.677	526.845	0.0014	0.0008	0.0015	0.0017
Story3	479.364	468.293	524.538	519.705	0.0016	0.0008	0.0016	0.0018
Story2	472.74	464.835	517.636	512.163	0.0016	0.0009	0.0017	0.0016
Story1	465.842	461.228	510.29	505.287	0.0015	0.0011	0.0016	0.0018
Nivel de Aislamiento	459.476	456.473	503.542	497.757

Tabla XII Resultados del analisis time-history para el sismo de Lima de 1966

En la Tabla XIII se aprecian los resultados del análisis time-history obtenidos con los cuatro casos de análisis sísmicos con el Sismo de Ancash de 1970. Respecto a los desplazamientos en el centro de masa se obtuvo un desplazamiento máximo de para el componente EW y para el componente NS. Respecto al drift de entrepiso, se obtuvo una deriva máxima de para el componente EW y para el componente NS. En ninguno de los cuatro casos de análisis se llegó a superar el valor de , por lo cual se puede concluir que para este sismo la estructura se mantendría dentro de la funcionalidad continúa establecida en los criterios HAZUS (FEMA, 2020).

	Desplazamiento en el centro de masa (mm)				Drift
Story	Ancash 1970 EW		Ancash 1970 NS		Ancash 1970 EW		Ancash 1970 NS
	XX	YY	XX	YY	XX	YY	XX	YY
Story4	400.863	402.496	358.467	362.45	0.0016	0.0009	0.0014	0.0013
Story3	394.076	398.665	352.424	356.951	0.0018	0.0010	0.0016	0.0014
Story2	386.658	394.424	345.837	351.119	0.0018	0.0010	0.0016	0.0012
Story1	379.104	390.312	339.167	345.883	0.0015	0.0011	0.0014	0.0013
Nivel de Aislamiento	372.715	385.757	333.356	340.462

Tabla XIII. Resultados del analisis time-history para el sismo de Ancash de 1970

En la Tabla XIV se aprecian los resultados del análisis time-history obtenidos con los cuatro casos de análisis sísmicos con el Sismo de Lima de 1974. Respecto a los desplazamientos en el centro de masa se obtuvo un desplazamiento máximo de para el componente EW y para el componente NS. Respecto al drift de entrepiso, se obtuvo una deriva máxima de para el componente EW y para el componente NS. En ninguno de los cuatro casos de análisis se llegó a superar el valor de , por lo cual se puede concluir que para este sismo la estructura se mantendría dentro de la funcionalidad continúa establecida en los criterios HAZUS (FEMA, 2020).

	Desplazamiento en el centro de masa (mm)				Drift
Story	Lima 1974 EW		Lima 1974 NS		Lima 1974 EW		Lima 1974 NS
	XX	YY	XX	YY	XX	YY	XX	YY
Story4	474.185	466.921	452.257	450.386	0.0012	0.0012	0.0012	0.0016
Story3	469.045	461.799	447.24	443.67	0.0014	0.0013	0.0013	0.0017
Story2	463.273	456.42	441.618	436.544	0.0015	0.0012	0.0014	0.0015
Story1	457.099	451.312	435.622	430.107	0.0014	0.0014	0.0013	0.0016
Nivel de Aislamiento	451.223	445.595	429.991	423.486

Tabla XIV Resultados del análisis time-history para el sismo de Lima de 1974.

En la Tabla XV se aprecian los resultados del análisis time-history obtenidos con los cuatro casos de análisis sísmicos con el Sismo de Arequipa de 2001. Respecto a los desplazamientos en el centro de masa se obtuvo un desplazamiento máximo de para el componente EW y para el componente NS. Respecto al drift de entrepiso, se obtuvo una deriva máxima de para el componente EW y para el componente NS. En ninguno de los cuatro casos de análisis se llegó a superar el valor de , por lo cual se puede concluir que para este sismo la estructura se mantendría dentro de la funcionalidad continúa establecida en los criterios HAZUS (FEMA, 2020).

	Desplazamiento en el centro de masa (mm)				Drift
Story	Arequipa 2001 - EW		Arequipa 2001 - NS		Arequipa 2001 - EW		Arequipa 2001 - NS
	XX	YY	XX	YY	XX	YY	XX	YY
Story4	471.015	456.541	323.638	319.159	0.0016	0.0008	0.0013	0.0009
Story3	464.327	453.21	318.116	315.358	0.0017	0.0009	0.0014	0.0009
Story2	457.004	449.477	312.047	311.546	0.0018	0.0009	0.0015	0.0008
Story1	449.41	445.767	305.832	308.063	0.0016	0.0011	0.0013	0.0012
Nivel de Aislamiento	442.582	441.302	300.515	303.137

Tabla XV Resultados del análisis time-history para el sismo de Arequipa de 2001

En la Tabla XVI se aprecian los resultados del análisis time-history obtenidos con los cuatro casos de análisis sísmicos con el Sismo de Ica de 2007. Respecto a los desplazamientos en el centro de masa se obtuvo un desplazamiento máximo de para el componente EW y para el componente NS. Respecto al drift de entrepiso, se obtuvo una deriva máxima de para el componente EW y para el componente NS. En ninguno de los cuatro casos de análisis se llegó a superar el valor de , por lo cual se puede concluir que para este sismo la estructura se mantendría dentro de la funcionalidad continúa establecida en los criterios HAZUS (FEMA, 2020).

	Desplazamiento en el centro de masa (mm)				Drift
Story	Ica 2007 EW		Ica 2007 NS		Ica 2007 EW		Ica 2007 NS
	XX	YY	XX	YY	XX	YY	XX	YY
Story4	360.765	359.715	312.573	307.553	0.0010	0.0013	0.0012	0.0008
Story3	356.603	354.164	307.378	304.214	0.0011	0.0014	0.0013	0.0008
Story2	351.932	348.317	301.822	300.791	0.0012	0.0012	0.0013	0.0008
Story1	346.964	343.068	296.16	297.603	0.0011	0.0013	0.0012	0.0011
Nivel de Aislamiento	342.377	337.515	291.239	293.125

Tabla XVI Resultados del análisis time-history para el sismo de Ica de 2007

Con estos resultados obtenidos, se observa en la Figura XIV que las derivas obtenidas mediante el análisis time-history y los cinco eventos sísmicos considerados en el análisis de la estructura son homogéneas y se mantienen por debajo de la deriva considerada como parámetro dentro HAZUS (FEMA, 2020) por lo cual se puede señalar que la estructura propuesta con aislamiento sísmico mejora su desempeño y se encuentra dentro del rango de la funcionalidad continua.

Figura XIV.- Derivas (Drift) obtenidas mediante el análisis time - history.

7. Conclusiones

· En el estudio se consideró una estructura esencial con un diseño sismorresistente basado en la norma peruana E.030. Inicialmente se verificó mediante un análisis inicial de tipo dinámico modal espectral que el máximo drift de la estructura es con un periodo de vibración de . Con este resultado se propuso un sistema de aislamiento sísmico en base a dispositivos con núcleo de plomo, calculado con la carga promedio según lo señala la norma peruana E.031.

· En la estructura con aislamiento se obtuvo un incremento significativo del periodo fundamental de la estructura casi en cinco veces el periodo original llegando a , resultado que implica que existe una disminución importante de las aceleraciones en los pisos superiores.

· En el análisis realizado con el espectro de seudoaceleración con se logró determinar que la estructura presenta un drift máximo de lo que significa una disminución de 57.45% con respecto a la deriva original, este resultado cumple con lo señalado en HAZUS (FEMA, 2020) que considera un drift máximo de para considerar la estructura dentro de la funcionalidad continua. El drift obtenido para la estructura con un análisis time-history, en ningún caso llegó a superar el drift considerado en HAZUS (FEMA, 2020), aspecto que implica que el desempeño estructural mejora considerablemente con deformaciones de entrepiso casi nulos frente a los eventos sísmicos escalados a sismos raros, lo que lleva a considerar que la estructura se encuentra en la funcionalidad continua en los casos de análisis considerados.

· En el análisis realizado con el espectro con se logró determinar que la estructura a nivel de base presenta en la interfaz de aislamiento, desplazamientos horizontales en la dirección y en la dirección lo cual supera en 12.87% el desplazamiento estático calculado mediante la norma En el análisis análisis time-history se logró determinar que la estructura a nivel de base presenta en la interfaz de aislamiento, desplazamientos variables entre y .

7. Referencias

[1] Constantinou, M. Whittaker, A. Kalpakidis, Y. Fenz, D. & Warn, G. Performance of seismic isolation hardware under service and seismic loading. Multidisciplinary Center for Earthquake Engineering Research. 2007, New York, USA.

[2] FEMA – HAZUS. HAZUS Earthquake Model Technical Manual. Versión 4.2 SP3, octubre. 2020. USA.

[3] Kammerer, A. Whittaker, A. & Constantinou. Technical Considerations for Seismic Isolation of Nuclear Facilities. NUREG/CR-7253. U.S. NNRC (United States Nuclear Regulatory Commision).2019, Universidad de Buffalo,USA.

[4] Kamrava, A. Seismic isolators and their types. Special Issue of Curr World Environ. 2015, Departament of Environment and Civil engineering . Shiraz University of Technology. Shiraz, Irán.

[5] Kelly, J. Earthquake-Resistant Design with Rubber. 1993, Department of Civil Engineering, University of California, USA

[6] Kelly, J. & Marsico, M. Seismic Isolation and Protection Systems. 2010, (The Journal of the Anti-Seismic Systems International Society – ASSIS, Vol. 1, Nro. 1). Mathematical Sciencies Publishers. Universidad de California. Berkeley. USA.

[7] Lancu, V. Gillich, G. & Vasile, O. Modelling and Characterization of Hybrid- Based Earthquake Isolation Systems. 2019, (Artículo). Researchgate. Bucharest, Romania.

[8] Lashgari, M. Comparative Study Base-Isolated and Fixed-Base Buildings Using a Damage/Cost Approach., 2014 (Tesis Doctoral). University of Nebraska. Lincoln, Nebraska, USA.

[9] Madera, I. Marulanda, J. & Thompson, P. Matrix and reinforcement materials for low-cost building isolators: an overview of results from experimental test and numerical simulations. 2019, Universidad del Valle. Santiago de Calí, Colombia. ISSN 2448-6736.

[10] Mayes, R. & Naeim, F. Design of Structures with Seismic Isolation. Earthquake Engineering Handbok, 2003. University of Hawaii.

[11] Naeim & Kelly, (1999). “Design of Seismic Isolated Structures: From Theory to Practice” Editorial John Wiley & Sons, Inc. Berkeley, California.

[12] Norma E.030. Norma Técnica E.030 Diseño Sismorresistente. (Reglamento Nacional de Edificaciones – RNE). Decreto Supremo No 355-2018-Vivienda. 2018, Lima-Perú.

[13] Norma E.031. Norma Técnica E.031 Aislamiento Sísmico. (Reglamento Nacional de Edificaciones – RNE). Decreto Supremo No 030-2019-Vivienda. 2019, Lima-Perú.

[14] Oikonomou, K. Constantinou,M. Reinhorn, A & Jr.L. Seismic isolation of high voltaje electrical power transformer. 2016, Technical Report, Multidisciplinary Center for Earthquake Engineering Research. MCCER.

[15] Skinner, R. Robinson, W. & McVerry, G. An Introduction to Seismic Isolation. 1993, Editorial Wiley. Wellington. New Zeland.

[16] Stojadinovic, B. Technical Considerations for Seismic Isolation of Nuclear Facility Structures. (s/f). Universidad de Berkeley, USA.

[17] Tavera, H. Bernal, I. Condori, C. Ordaz, M. Zevallos, A. Ishizawa, O. Evaluación del Peligro Sísmico en Perú. 2014, Instituto Geofísico del Perú. Lima – Perú.

[18] Usta, P. Investigation of a Base-Isolator System’s Effects on the Seismic Behavior of a Historical Structure. 2021, University of Applied Science. Ispart, Turquía.

[19] Wamanrao, P. & Narayan, M. Sustainability of Structure Using Base Isolation Technique for Seismic Protection. (Artículo). 2015, International Journal of Innovative Research in Science, Engineering and Technology. Pune, India.

[20] Zayas, V. Estándar de Aislamiento Sísmico para la Funcionalidad Continua. 2017, COINESED 2017, I Congreso Internacional de Estructuras de Edificación, Lima – Perú.

[21] Zellat & Kadri. Influence of seismic isolation system on brigde responses. 2015, (Artículo). Lima-Perú.

[22] Constantinou, M. Whittaker, A. Kalpakidis, Y. Fenz, D. & Warn, G. Performance of seismic isolation hardware under service and seismic loading. Multidisciplinary Center for Earthquake Engineering Research. 2007, New York, USA.

[23] FEMA – HAZUS. HAZUS Earthquake Model Technical Manual. Versión 4.2 SP3, octubre. 2020. USA.

[24] Kammerer, A. Whittaker, A. & Constantinou. Technical Considerations for Seismic Isolation of Nuclear Facilities. NUREG/CR-7253. U.S. NNRC (United States Nuclear Regulatory Commision).2019, Universidad de Buffalo,USA.

[25] Kamrava, A. Seismic isolators and their types. Special Issue of Curr World Environ. 2015, Departament of Environment and Civil engineering . Shiraz University of Technology. Shiraz, Irán.

Nota contribución de los autores:

1. Concepción y diseño del estudio

2. Adquisición de datos

3. Análisis de datos

4. Discusión de los resultados

5. Redacción del manuscrito

6. Aprobación de la versión final del manuscrito

KN ha contribuido en: 1, 2, 3, 4, 5 y 6.

GV ha contribuido en: 1, 2, 3, 4, 5 y 6.

VN ha contribuido en: 1, 2, 3, 4, 5 y 6.

Nota de aceptación: Este artículo fue aprobado por los editores de la revista Dr. Rafael Sotelo y Mag. Ing. Fernando A. Hernández Gobertti.

---

[1] Dra. Universidad Nacional del Santa, k.niquen14@gmail.com,

ORCID iD: https://orcid.org/0009-0002-3373-5479

[2] PhD. Universidad de San Martin de Porres (Perú), gvillarrealc@usmp.pe,

ORCID iD: https://orcid.org/0000-0003-1768-646X

[3] Dr. Universidad Nacional de Tumbes (Perú), vni1807@gmail.com

ORCID iD: https://orcid.org/0000-0001-6404-7789